
Moles:
CONTENTS
Counting Atoms − The Chemist's Impossible Dream
WHY COUNT ATOMS?
When we represent a chemical reaction using a balanced equation we are indicating the number of particles that react together.
e.g. 2H2 + O2 → 2H2O
Here we are stating that two molecules of hydrogen react with one molecule of oxygen to form two molecules of water. In addition, the formula of a compound indicates the number of atoms (or ions) present in the compound.
e.g. CO2 means that a molecule of carbon dioxide contains one atom of carbon, and two of oxygen.
Numbers are important to chemists. When chemists talk about 'how much' (of a substance), they are talking about numbers rather than masses or volumes.
PROBLEM: Atoms are very, very, very, very small and the numbers of them in a small quantity is so vast that it is not possible to count them directly.
Remarkably, scientists have worked out a method of counting atoms by weighing them on a balance.
RELATIVE ATOMIC MASS, Ar
From experiments, we know the relative atomic mass of different elements. Relative atomic mass means how heavy they are compared to each other. The unit mass for all atoms to be compared to has been chosen as 1/12th the mass of a carbon-12 atom (1/12th of 12 is of course 1!). The relative atomic masses of elements are shown in the periodic table (the larger number).
| e.g. | Oxygen, O | Ar = 16 | This means that on average, an oxygen atom is 16 times heavier than the defined unit mass. |
| e.g. | Gold, Au | Ar = 197 | This means that on average, a gold atom is 197 times heavier than the defined unit mass. |
The reason that we say it is 'on average' is because relative atomic mass is a weighted average of all isotopes of an element.
DEFINITION: Relative Atomic Mass, Ar
The relative atomic mass, Ar is the average mass of an atom of that element compared to 1/12th the mass of a carbon-12 atom.
Relative molecular mass (Mr) is simply the sum of the relative atomic masses of the compound or element, e.g. O2 = 2 x 16 = 32
COUNTING BY WEIGHING
Relative masses are very important because they enable us to weigh out (on a balance) equal numbers of particles of different substances.
Counting by weighing is commonly used in normal life: e.g. in banks, coins are weighed to count them, as long as we know the mass of a single coin.
We are also familiar with the use of words to indicate numbers. e.g. a dozen = 12, a million = 1,000,000.
In chemistry, atoms are so small that we need a very, very large number.
A MOLE = 6 x 1023 particles (Avogadro's Number - more accurately 6.02 x 1023)
=600,000,000,000,000,000,000,000
=Six hundred thousand million, million, million
DEFINITION: Mole
Actually, a mole is the unit of 'amount of substance' (just as the gram is the unit of mass). 1 mole is the amount of substance that contains 6 x 1023 particles of the substance.
Why this number?: The mole provides the link between the mass of a substance and the number of particles it contains.
1 mole of any particle has a mass equal to its Ar, in grams.
This just means that the relative mass of any element is equal to the mass of 1 mole of that element in grams. So, any time you see the words 'relative atomic mass' or 'relative molecular mass', you can substitute it for 'mass of 1 mole', if it makes it easier for you to understand.
(Just as gram is shortened to g, mole is shortened to mol)
e.g. 6 x 1023 nitrogen atoms has a mass of 14g, or 1 mole of nitrogen atoms has a mass of 14g [Ar(N) = 14]
e.g. 0.5 moles of NaOH are in 20g of pure NaOH [1 mole of NaOH is 40g as Mr(NaOH) = 23 + 16 + 1 = 40].
THE FORMULA (FOR PURE SUBSTANCES)
`"Amount of Substance (in moles, mol)" = "Mass (in grams)"/"Relative mass"`
OR
`n = m/M_r`
You can rearrange this formula to find mass or relative mass as well:
`n = m/M_r`
`m = n xx M_r`
`M_r = m/n`
FINDING THE PERCENTAGE COMPOSITION OF A GIVEN COMPOUND
Use this equation to find the percentage composition of an element in a compound:
`"Percentage of Element" = ("Number of Atoms " xx " Relative Atomic Mass of Element")/"Relative Molecular Mass of Compound" xx 100`
e.g. Find the percentage composition of each element in ethanol (C2H5OH)
1 mole of ethanol (C2H5OH) contains:
| 2 moles of carbon | = 2 x C |
| = 2 x 12 | |
| = 24g |
|
| 6 moles of hydrogen | = 6 x H |
| = 6 x 1 | |
| = 6g |
|
| 1 mole of oxygen | = 1 x O |
| = 1 x 16 | |
| = 16g |
Relative Molecular Mass = 46
| % of Carbon: | = {2 x 12⁄46} x 100 |
| = 52.2% |
|
| % of Hydrogen: | = {6 x 1⁄46} x 100 |
| = 13.0% |
|
| % of Oxygen: | = {1 x 16⁄46} x 100 |
| = 34.8% |
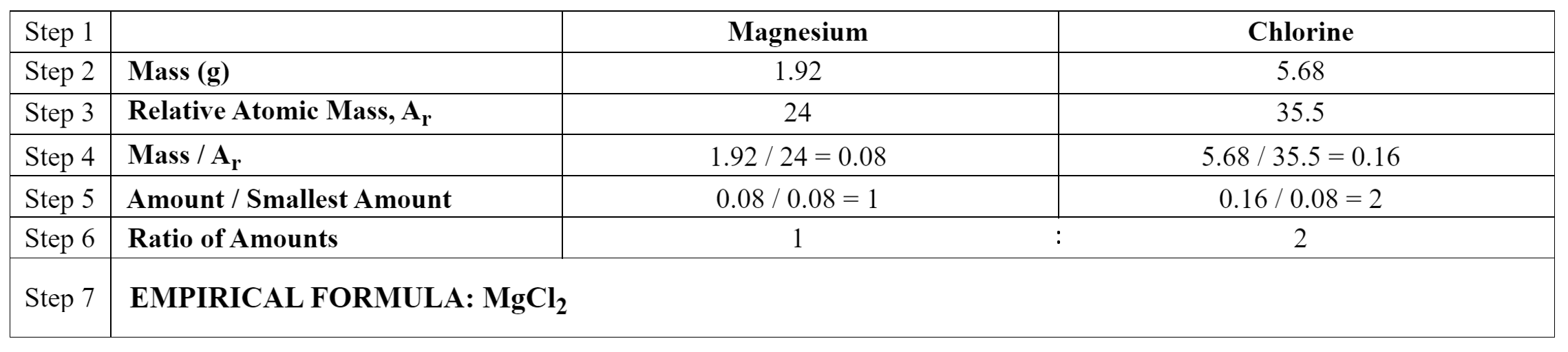
EMPIRICAL FORMULA
The empirical formula of a compound is the simplest positive integer (whole number) ratio of atoms of each element in that compound. For example, glucose has a molecular formula of C6H12O6, but its empirical formula is CH2O.
The empirical formula of a compound can be calculated if the reacting masses are known, using this method:
- Write down the elements reacting
- Write down the mass of each of the elements reacting
- Write down the Ar of each of the elements reacting
- Divide the masses by the Ar values
- Divide by the smallest number
- Write down the ratio of the elements reacting
- Write down the formula
e.g. Calculate the empirical formula of a compound made by combining 1.92g of magnesium with 5.68g of chlorine.
PERCENTAGE YIELD
Percentage yield is a way of comparing how much product you make (called the actual yield) with the theoretical maximum you can make (called the predicted yield or theoretical yield). The closer the percentage yield is to 100%, the closer the actual yield is to the predicted yield. It is impossible to get 100% yield because some reactants or products are always lost in the reaction.
The percentage yield can be calculated using the following formula:
`"Percentage Yield" = "Actual Yield"/"Predicted Yield" xx 100`
CONSERVATION OF MASS
The law of conservation of mass, discovered by Antoine Laurent Lavoiser, states that matter can be neither created nor destroyed. This means that in a closed system, the mass of the system must remain constant over time.
If you heat a piece of copper in air, it reacts with oxygen from the air and forms of copper oxide. If you measure the mass of the metal before and after the reaction, you will find that the mass has increased. This increase in mass is equal to the mass of the oxygen which has covalently bonded to the copper during the reaction. This can be shown on a balance scale:
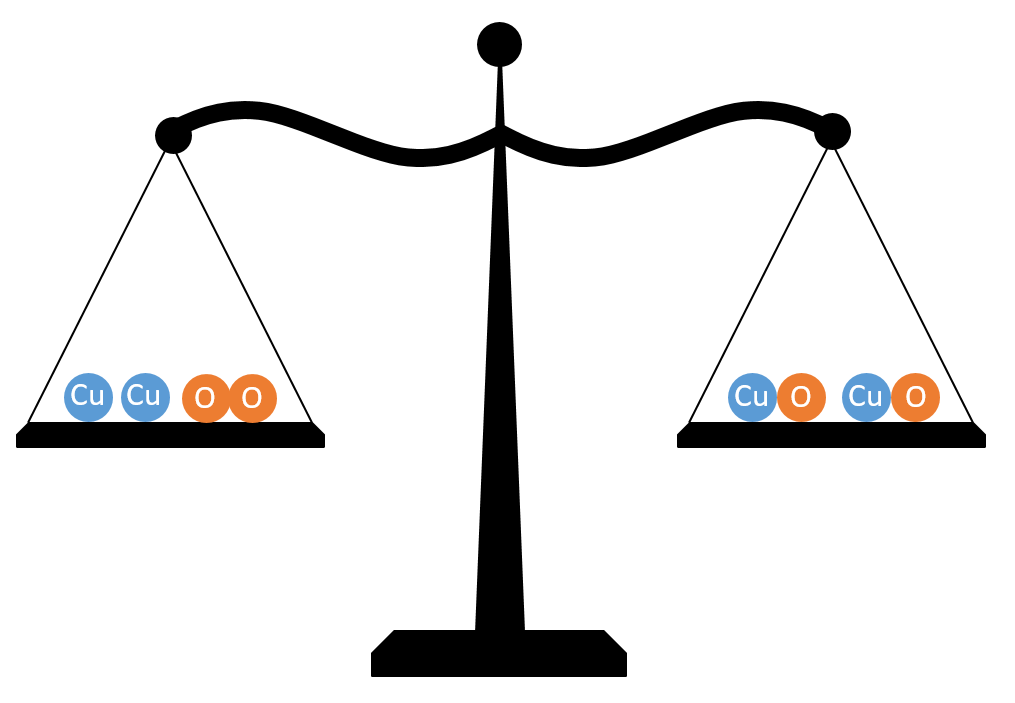
The atoms have moved about, but there are still the same number after the reaction as there were before (there were 2 copper atoms before the reaction and 2 copper atoms after; there were 2 oxygen atoms before the reaction and 2 oxygen atoms after). If there are the same number of atoms at the end as there were at the start, there must be the same total mass, so the balance scales are balanced.
REACTING MASS CALCULATIONS
As we know that atoms can be neither created nor destroyed (See Conservation of Mass) and we know the relative masses of different elements, we can predict the masses of reactants and products involved in chemical reactions.
e.g. What mass of Fe3O4 is produced when 140g of iron reacts with excess steam?
3Fe(s) + 4H2O(g) → Fe3O4 (s) + 4H2 (g)
\[\text{Step 1:} \\
\begin{align}n(Fe) & = \frac{m}{M_r} \\
& = \frac{140}{56} \\
& = 2.5 mol\end{align}\]
\[\text{Step 2:} \\
\begin{align}\text{Using equation, } n(Fe_3O_4) & = \frac{2.5}{3} \\
& = 0.833 mol \text{ (3 s.f.)}\end{align}\]
\[\text{Step 3:} \\
\begin{align}m(Fe_3O_4) & = n \times M_r \\
& = 0.833 x 232 \\
& = 193g \text{ (3 s.f.)}\end{align}\]
MOLAR CONCENTRATION (MOLARITY)
Many chemical (and biological) reactions take place in solution. When conducting an experiment it is important to know how concentrated a solution is, or how much of a reactant is dissolved in it.
Volume:
In solution calculations, the volumes of solvent are crucial, and the correct unit must be used - cubic decimetres (dm3). A cubic decimetre is a cube with sides of length 10cm.
1dm3 = 1000cm3
1dm3 = 1 litre (1000ml)
Concentration:
The concentration is the amount of substance dissolved in a solution per unit volume, i.e. the number of moles per decimetre cubed (mol/dm3).
To calculate the concentration of solutions we use the following formula:
`"Concentration (in mol/dm"^3")" = "Amount (in moles)"/("Volume (in dm"^3")")`
OR
`c = n/V`
When using this formula, always remember to convert the volume to dm3.
This formula is often rearranged as `n = cV` to calculate the number of moles in a solution.
Making Solutions of Known Concentration:
To make up a solution of known concentration, a given amount of substance (solute) is dissolved into a volume of liquid (solvent). E.g. if 1 mole of solute is dissolved in 1dm3 of solvent, the concentration is 1.00mol/dm3. Varying the amount of solute and/or solvemt allows the preparation of solutions with different concentrations.
As solids are usually weighed, the mass of solid is often used to measure the amount of solute. Here, the concentration and pure substance equations are used together to calculate the concentration.
e.g. Calculate the concentration of a solution containing 100g CaCO3 in 1.00dm3 of solution.
\begin{align}M_r(CaCO_3) & = 40 + 12 + (3 \times 16) \\ & = 100\end{align}
\begin{align}n(CaCO_3) & = \frac{m}{M_r} \\ & = \frac{100g}{100} \\ & = 1.00 moles\end{align}
\begin{align}c & = \frac{n}{V} \\ & = \frac{1.00}{1.00} \\ & = 1 mol/dm^3 \text{ or } 1M\end{align}
MOLAR GAS VOLUME
Avogadro's Law: Equal volumes of gas at the same temperature and pressure contain an equal number of molecules.
Therefore, 1 mole of any gas at room temperature and pressure will occupy the same volume. This is the Molar Gas Volume (Vm)
`"Volume of Gas (in dm"^3")" = V_m xx "Number of Moles"`
`V_m` is 24 at room temperature and pressure (i.e. At room temperature and pressure, 1 mole of gas occupies 24dm3).
Therefore, at room temperature and pressure:
`V = 24n`
MOLES QUIZ
Back to Chemistry Home